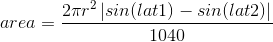Kev here: After an online, shall we say, discussion about how much of a map showed average temperatures, I felt I needed a really intuitive way of depicting just that. As it became increasingly clear, it's really difficult to eyeball something like this:
...and conclusively state that there are more "warmer than average" than "cooler than average" areas, especially when taking into account the crazy distortions of the equirectangular projection. To be fair, the discussion was mainly based on maps using the Kavrayskiy VII projection, which has its own distortions, but I digress.
So what to do? I wanted to create an animation that was short, simple, and intuitive but without involving figures like percentages and square areas, etc. It came to me that it would look cool to see the colours on the map pick themselves up and organise themselves into a column showing their respective proportions.
This would mean I'd need to read each pixel, one at a time, and work out its area, then slide it across and position it in a column. The tool best suited for this sort of thing would be Processing, which is a special purpose animation language.
So, the general idea is that I map (that's mathematically map, not geometrically map) a colour to a temperature value (conveniently, ClimateReanalyzer provides a legend at the bottom with all the colours in it!) and then run through them incrementally finding in the map (the geographical one this time) the pixels with that colour, delete them, and steadily move them at a certain speed and direction until they arrive at the right point. Simple!
Yeah, like I said, "simple."
So, the algorithms I used the most are: one to work out the area of a pixel from the equirectangular projection and one for the acceleration/deceleration motion of the pixel. Everything else was mainly data structure manipulation to remember where pixels are, where they are going to, and how many are already at their destination.
The equirectangular projection, although not the most aesthetically pleasing or the least distorted, has the great advantage that the area of each pixel is super easy to calculate. It only depends on the latitude: you just work out the area of a ring of latitude around the planet and then divide it by the number of pixels horizontally, in this case 1040.
As the projection's y axis is merely the latitude, we know how many degrees per pixel (simply divide 180 by the height of the map), so we can easily work out lat1 and lat2 from the y coordinate. Just add in the radius of the Earth, and Robert's your mother's brother.
To make the movement of the pixels as natural as possible, I used what is known as an easing function. The one I chose is the in/out cubic function, which produces motion that looks like this:
There are many to choose from, including ones with bounce and elastic motion.
After much experimentation, I created a first draft:
But I felt the single column didn't highlight the near-average colours very well; they were quite washed out and hard to distinguish. With the help of Marlo and her top-notch palette modification skills, we tried modifying the colours so that the bar showed more contrast, but we soon came to the conclusion that unless we went with some quite psychedelic colours, the single bar wasn't going to work very well.
So, I decided to try three bars: one for the "lower than average" temperatures, one for the "average temperatures," and one for the "higher than average" temperatures. As the average temperatures were just one colour, the same animation wasn't going to work very well, so I went with a right-to-left swipe, resulting in the finished article: