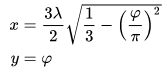Hi, Kev here. Last week I described how to load the gridded global temperature data into memory; this week I'll describe how to render it on a map.
First, let's get some structural bits done. I'm going to render one month per frame, which simply means I'll need a variable to hold the month number and another for the year. I'll set them both to the start date. As the contents of these variables will need to be retained between frames, the variables will need to be defined outside the draw() function like so:
int month = 1;
int year = 1880;
void draw()
{}
Inside the draw() function, I increment the month number every frame, and when it gets to greater than 12, I then increment the year and set the month back to 1.
void draw()
{
println(month + " " + year);
month++;
if(month > 12)
{
month = 1;
year++;
if(year > 2017)
exit();
}
}This should output:
...
7 1880
8 1880
9 1880
10 1880
11 1880
12 1880
1 1881
2 1881
3 1881
...
...in the console. These are our keys for the HashMap.
I then set the size to HD (1920 by 1080) like so:
void setup()
{
loadData();
size(1920,1080);
}So now we are good to go.
I'm now simply going to plot the data in a square grid. First thing's first: I need to get the temperature data given the month and year. So, just before I increment the month, I add this code:
String dataKey = month + " " + year; int[][] temperatureGrid = data.get(dataKey);
temperatureGrid is a 37 by 73 array, which means we can loop through it like so:
for(int x = 0; x < 37; x++)
{
for(int y = 0; y < 73; y++)
{
print( temperatureGrid[x][y] + " ");
}
println();
}
This prints out all the data to the console
Now I'll draw dots for each temperature on the screen in a grid. For the colours I use a function called lerpColor(). "lerp" is a contraction of "linear interpolation". It merely means, given two numbers, find me a number in between. So, to find a number three quarters of the way between 10 and 20, you'd give a lerp function: 10, 20, 0.75 and it'd spit out 17.5. For lerpColor() you give it two colours and a fraction, and it'll spit out a colour in between those colours.
Colours are represented as three numbers between 0 and 255. Each of those numbers are the level of red, green, and blue respectively. So color(255,0,0) is red, color(0,0,255) is blue, and color(255,255,255) is white.
I'm colouring the above normal temperatures with red and the below normal temperatures with blue. Temperatures near normal are white.
I replaced print( temperatureGrid[x][y] + " "); above with the following:
float temperature = temperatureGrid[x][y]/100.0; color tempColour; if(temperature >= 0) tempColour = lerpColor(color(255,255,255), color(255,0,0), temperature); else tempColour = lerpColor(color(255,255,255), color(0,0,255), -temperature); stroke(tempColour); point(x,y);
This creates the following:
Making pretty good progress with only a few lines of code! Evidently, I have got my x and y coordinates around the wrong way. Let's fix that and make them pixels larger:
for(int x = 0; x < 73; x++)
{
for(int y = 0; y < 37; y++)
{
float temperature = temperatureGrid[y][x]/100.0;
color tempColour;
if(temperature >= 0)
tempColour = lerpColor(color(255,255,255), color(255,0,0), temperature);
else
tempColour = lerpColor(color(255,255,255), color(0,0,255), -temperature);
noStroke();
fill(tempColour);
int x10 = x * 10;
int y10 = y * 10;
rect(x10, y10, x10 + 10, y10 + 10);
}
}Giving us:
Lovely. If you squint, you can make out the continents! Hang about---why are they flat blue? Ah! missing values are marked as -9999, so therefore, they are blue as that's very much below normal. I'll mark those as grey color(150,150,150). As the colour code is getting cumbersome, I'll extract it out as a function like so:
color getColour(float temperature)
{
if (temperature < -90)
return color(150,150,150);
color tempColour;
if(temperature >= 0)
tempColour = lerpColor(color(255,255,255), color(255,0,0), temperature);
else
tempColour = lerpColor(color(255,255,255), color(0,0,255), -temperature);
return tempColour;
}
Ok, that looks pretty good. But squares greatly distort the area of each segment of the earth's surface. What we need is a proper sphere projecting function of which there is no end of choice.
My favourite is the fabulously named Kavrayskiy VII projection:
The projection is defined as:
DON'T PANIC
This is really very simple. It just looks complicated because of all the Greek symbols and what-not. λ (lambda) is the longitude, and φ (phi) is the latitude in radians. I'll stick with radians, as computers by default use radians, so no need to convert.
Right, from the get-go I can see that the y coordinate is merely the latitude. Happy days. The x coordinate is calculated as follows in code:
float x = (3.0 * lng / 2.0) * sqrt( (1.0 / 3.0) - sq(lat / PI));
The sqrt() and sq() functions are square root and square respectively.
Processing has the type PVector, which allows us to handle an x,y coordinate pair, which means I can create a function like so:
PVector getKavrayskiyVII(float lat, float lng)
{
float x = (3.0 * lng / 2.0) * sqrt( (1.0 / 3.0) - sq(lat / PI));
return new PVector(x, lat);
}Which returns the x and y coordinates of a given longitude and latitude.
The problem I have now is that I'm looping through the x and y coordinates when I now need to loop through the longitude and latitude angles. The data is for 5° by 5° segments of the surface or π/36 radians. So my loops now need to look like:
float step = PI/36.0;
float halfPi = PI/2.0;
int latCount = 0;
int lngCount = 0;
for(float lng = -PI; lng < PI; lng+=step)
{
for(float lat = halfPi; lat > -halfPi; lat-=step)
{
float temperature = temperatureGrid[latCount][lngCount]/100.0;
latCount++;
}
latCount = 0;
lngCount++;
}
As I am working out four points surrounding a point on a sphere, I get the top-left, top-right, bottom-left, and bottom-right points like so:
float halfStep = step/2.0; PVector tl = getKavrayskiyVII(lat + halfStep, lng - halfStep); PVector tr = getKavrayskiyVII(lat + halfStep, lng + halfStep); PVector bl = getKavrayskiyVII(lat - halfStep, lng - halfStep); PVector br = getKavrayskiyVII(lat - halfStep, lng + halfStep);
To draw a four sided irregular polygon I'm using the quad() function where s scales it to a nice size:
float s = 170; quad ( tl.x * s, -tl.y * s, tr.x * s, -tr.y * s, br.x * s, -br.y * s, bl.x * s, -bl.y * s );
Which generates:
How about that, eh?
The complete code can be found on github. Fork it and have fun!
Next week, I'll overlay it on the map of the earth from above.